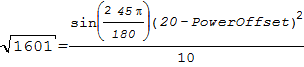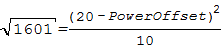Latest revision as of 00:49, 21 February 2014

The actual guide for Telescience is written horribly. I'm remaking it.

Welcome to Telescience, the room where you teleport things/people/bombs you aren't supposed to have into places said things/people/bombs aren't supposed to be, or use it for legitimate purposes.

Tha' Hell is This New Fangled Telescience Stuff That Runs on That Electricial-Tricity?

Telescience_room

The Telescience Lab

Telescience is a single room at the south end of the Research department hallway.

This area focuses on teleportation, both sending and receiving. It is equipped with a Telepad, a secure room to teleport people and things in and out of, and several handheld GPS readers.

Telescience is imprecise, but potentially extremely useful. Try teleporting GPSs to see where they go, and then from there you can move objects or people back and forth from your lab. Like all science rooms, experimentation is key!

Holy Shit, I Will be the Ruler of Space and Time!

A word of warning. Telescience requires math. Of course, as a scientist, you have a good understanding of mathematical knowledge and projectile trajectory, right?

The telepad console has 4 settings:

Bearing (measured in degrees, can be changed from 0 to 360)
Elevation (measured in degrees, can be changed from 0 to 90)
Power (measured in integer units, can be changed from 5 to 100 provided you have enough Bluespace Crystals at hand, from 5 to 20 by default)
Sector (defines the z-level which we are beaming to or from, default is 1, corresponding to the main station z-level).

Together, these 4 settings define the coordinates whatever or whoever is on the telepad will find themselves after you push the Send button on the console via the following equation:

where

For non-mathy people, think of the telepad as a cannon. Your bearing is the angle you rotate the cannon to, your elevation is the angle you point your barrel at the sky, the power is how hard you're going to shoot the projectile, and the sector has no analogy here.

For mathy people, think the same thing, but keep in mind the following

There is no drag/air resistance to calculate
The cannon's aiming is perfect
The terrain is perfectly flat
The gravitational acceleration in this world is 10 units/second^2
0° is north.

Alright, I'm ready to teleport a bomb into the AI Core!

Not so fast. It would be way too easy to use telescience if the equations were that simple! To compensate, Nanotrasen has added some features to make telescience more inaccurate! Basically, there are little "offsets" that get added to the values you input. For now, we're just going to deal with two offsets, because that is how the teleporter currently is. Here they are:

The Power Offset. This is a number x such that -4 ≤ x ≤ 0. This will be added to the power that you input for the teleporter to use.
The Bearing Offset. This is a number x such that -10 ≤ x ≤ 0. This will be added to the bearing that you input for the teleporter to use.

So, in reality, here are the real equations we will be using with telescience:

and

To make things even more fun, every 20-40 uses the teleporter will have to be "recalibrated," which randomly changes the offsets. Yay!

Ugh. Fine. Just tell me what the hell I need to do!

My pleasure. Basically, we're going to substitute known values into the equations above and solve for the offsets. It's really not that hard. Here's what we're gonna do:

Grab a GPS and teleport it to get a DestinationX and a DestinationY value, plus a Distance value.
Plug said values into the equations above, along with the bearing you used to teleport the GPS.
Solve for the bearing offset.
Plug the power and elevation you teleported the GPS with into the distance equation above.
Solve for the power offset.

Let's get started, shall we?

Step 1, in detail

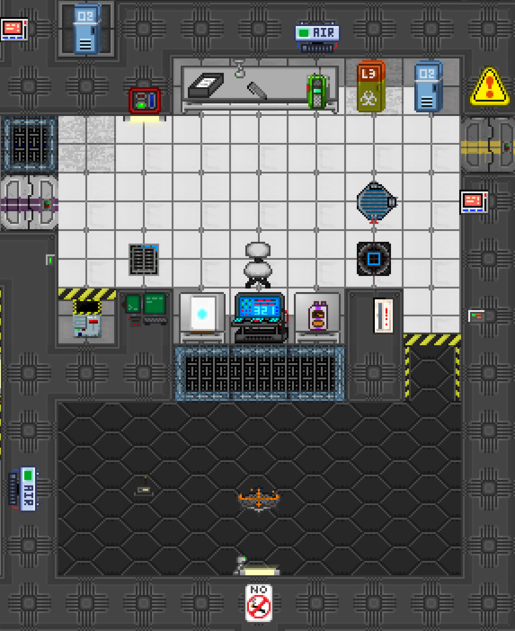
Grab two GPS's from the table to your left. Look at the image provided if you are retarded and can't find them.
Take one and place it on the telepad. Again, look at the image provided if you have no idea what I'm talking about.
Now, go to the telescience computer and use it. Set the bearing and elevation to whatever the hell you want, but 0° for the bearing and 45° for the elevation makes the following steps easier.
Set the power to 20 or higher.
Now hit send
Use the GPS in your hand. This will give you a list of GPS's. Look for the one that is in a different room than the others.
Write down the coordinates somewhere
To calculate the distance the GPS traveled, we use the following equation

We use 185 and 97 because the telepad is located at 185, 97.

Write down that distance somewhere.

Steps 2-3, in detail

Alright, so now you have some values. Time to plug that shit into the equations.

For the purposes of this article, the GPS that we teleported ended up at 184, 137. The distance the GPS traveled is 40.01249804748511...ish, or the square root of 1,601. The bearing, elevation, and power were 0, 45, and 20, respectively.

First thing we're going to do is plug the numbers we have into the DestinationX equation to determine the bearing offset.

Subtract 185 from both sides

Divide both sides by 40.01249804748511

Take the arcsin of 0.02499479361892

By default, my calculator calculates stuff in radians. To convert to degrees, multiply by 180/pi

And we end up with a value of 1.432245340659903. Multiply that number by -1, and you have your bearing offset. It's either -1 or -2!

Steps 3-4, in detail

Now to solve for the power offset.

First, plug in your values. We know the distance is equal to the square root of 1601, so no need to calculate that again. Elevation was 45, and the Power was 20.

Well, the sine of 90pi/180 radians, or pi/2, is 1, so we can cut that shit out of the equation

Multiply both sides by 10

Take the square root of both sides

Well, we know that PowerOffset must be a negative number. Therefore we can remove those bars and multiply the left side of the equation by -1.

Add 20 to both sides

Which is equal to -0.0031242678450383. Therefore, the power offset is 0.

Challenges for the Robust in All of Us

Be useful and teleport dead bodies to Genetics for cloning, or injured crew straight to Medbay for treatment!
Teleport an Engineering Cyborg straight to a hull breach!
Borrow all the Chef's donuts!
Teleport the last remaining revhead into the Brig for implanting!
Find the remaining Bananium ore and construct a H.O.N.K. mech for the Clown!
Teleport the Nuclear Device around during a Nuclear Operatives -round! Bonus points if it's right after they stick in DAT FUKKEN DISK and before they input the code! Double bonus points for teleporting it to the derelict!
Teleport a bomb onto a malfunctioning AI's core!
Teleport the WGW reader into LORD SINGULOTH!

@@ Line 1: / Line 1: @@
-{{Needs revision| reason = Out of date}}
+=The actual guide for Telescience is written horribly. I'm remaking it.=
 Welcome to Telescience, the room where you teleport things/people/bombs you aren't supposed to have into places said things/people/bombs aren't supposed to be, or use it for [[Beyond the impossible|legitimate purposes]].
@@ Line 41: / Line 41: @@
 ===Alright, I'm ready to teleport a bomb into the AI Core!===
-Not so fast. It would be way too easy to use telescience if the equations were that simple! To compensate, Nanotrasen has added some features to make telescience more inacurate! Basically, there are little "offsets" that get added to the values you input. For now, we're just going to deal with two offsets, because that is how the teleporter currently is. Here they are:
+Not so fast. It would be way too easy to use telescience if the equations were that simple! To compensate, Nanotrasen has added some features to make telescience more inaccurate! Basically, there are little "offsets" that get added to the values you input. For now, we're just going to deal with two offsets, because that is how the teleporter currently is. Here they are:
 *The Power Offset. This is a number x such that -4 ≤ x ≤ 0. This will be added to the power that you input for the teleporter to use.
@@ Line 55: / Line 55: @@
 *[[File:Telescience real distance equation.png]]
-To make things even more fun, every 20-40 uses the teleporter will have to be "recalibrated," which randomly creates the offsets again!
+To make things even more fun, every 20-40 uses the teleporter will have to be "recalibrated," which randomly changes the offsets. Yay!
 ===Ugh. Fine. Just tell me what the hell I need to do!===
@@ Line 61: / Line 61: @@
 My pleasure. Basically, we're going to substitute known values into the equations above and solve for the offsets. It's really not that hard. Here's what we're gonna do:
-. Grab a GPS and teleport it to get a DestinationX and a DestinationY value, plus a Distance value.
+#Grab a GPS and teleport it to get a DestinationX and a DestinationY value, plus a Distance value.
+#Plug said values into the equations above, along with the bearing you used to teleport the GPS.
-. Plug said values into the equations above
+#Solve for the bearing offset.
+#Plug the power and elevation you teleported the GPS with into the distance equation above.
-. Plug the power, elevation, and bearing you teleported the GPS with into the equations above
+#Solve for the power offset.
-. Solve for the offsets
 Let's get started, shall we?
-###Step 1, in detail###
+==Step 1, in detail==
 [[File:Telescience Room.png|thumb|515px|alt=Telescience Room|link=Telescience|This thing.]]
 #Grab two GPS's from the table to your left. Look at the image provided if you are retarded and can't find them.
 #Take one and place it on the telepad. Again, look at the image provided if you have no idea what I'm talking about.
-#Now, go to the telescience computer and use it. Set the bearing and elevation to whatever the hell you want, but 0° for the bearing and 45° for the elevation makes the following steps easier. '''Set the power to 20 or higher. No exceptions.'''
+#Now, go to the telescience computer and use it. Set the bearing and elevation to whatever the hell you want, but 0° for the bearing and 45° for the elevation makes the following steps easier.
+#'''Set the power to 20 or higher.'''
+#Now hit send
+#Use the GPS in your hand. This will give you a list of GPS's. Look for the one that is in a different room than the others.
+#Write down the coordinates somewhere
+#To calculate the distance the GPS traveled, we use the following equation
+[[File:Telescience gps distance equation.png]]
+We use 185 and 97 because the telepad is located at 185, 97.
+Write down that distance somewhere.
+==Steps 2-3, in detail==
+Alright, so now you have some values. Time to plug that shit into the equations.
+For the purposes of this article, the GPS that we teleported ended up at 184, 137. The distance the GPS traveled is 40.01249804748511...''ish'', or the square root of 1,601. The bearing, elevation, and power were 0, 45, and 20, respectively.
+First thing we're going to do is plug the numbers we have into the DestinationX equation to determine the bearing offset.
+[[File:Telescience plugged distanceX equation.png]]
+Subtract 185 from both sides
+[[File:Telescience plugged distanceX equation step 1.png]]
+Divide both sides by 40.01249804748511
+[[File:Telescience plugged distanceX equation step 2.png]]
+Take the arcsin of 0.02499479361892
+[[File:Telescience plugged distanceX equation step 3.png]]
+By default, my calculator calculates stuff in radians. To convert to degrees, multiply by 180/pi
+[[File:Telescience plugged distanceX equation solved.png]]
+And we end up with a value of 1.432245340659903. Multiply that number by -1, and you have your bearing offset. It's either -1 or -2!
+==Steps 3-4, in detail==
+Now to solve for the power offset.
+First, plug in your values. We know the distance is equal to the square root of 1601, so no need to calculate that again. Elevation was 45, and the Power was 20.
+[[File:Telescience plugged distance equation.png]]
+Well, the sine of 90pi/180 radians, or pi/2, is 1, so we can cut that shit out of the equation
+[[File:Telescience plugged distance equation step 1.png]]
+Multiply both sides by 10
-'''Now this next part requires some math and a calculator supporting square roots and inverse trigonometric functions, specifically asin() and atan().''' If you're incapable of math, ask yourself what the hell are you doing in the Research Division of the most high-tech space station ever built, and apply to [[Head of Personnel]] for the [[Clown]]'s job.
+[[File:Telescience plugged distance equation step 2.png]]
-First, let's find the power offset. It is most simply done by setting elevation to 45. Elevation set to 45 sets the sin(2*elevation) to 1 so the equation for the distance simplifies to (power^2)/10. For example if you teleport something with power 20, it should be (20^2)/10 = 40 tiles away. That's where the power offset comes in, as the GPS will actually be in ((power-offset)^2)/10, so, using the previous example and if the offset is, say, -4, the GPS will be actually ((20-4)^2)/10  = (16^2)/10 = 25.6 (rounded to 26) tiles away. So, to find out the power offset, you need to teleport the GPS with 45 elevation and see how far away it actually flies. Let's designate the GPS coordinates as X and Y, and the telepad coordinates as Xt and Yt. Then the formula for the distance from the telepad to the GPS is:
+Take the square root of both sides
-*distance = sqrt((Xt - X)^2 + (Yt - Y)^2)
-and the equation for actually finding the offset is:
-*((power-offset)^2)/10 = distance,  therefore (power-offset)^2 = distance*10,  therefore '''power-offset = sqrt(distance*10)'''.
-So, to recollect, to find the power offset you need to:
+[[File:Telescience plugged distance equation step 3.png]]
-*Teleport the GPS with settings 0 bearing, 45 elevation, 20 power.
-*Using another GPS find out how far did it go in both x and y directions (say, it travelled X tiles on x axis and Y on y axis).
-*Calculate the distance from the telepad to the GPS as sqrt(X^2 + Y^2)
-*Multiply it by 10 and extract sqare root.
-*What you see at your calc now is power minus offset. As the power was set to 20, to find offset, you need to substract the number you've got from 20. So, for example, if you got roughly 17, the offset is 3 (remember it can be only integer).
-{{Item
- |bgcolor1 = #ccccee
- |bgcolor2 = #ddddff
- |name = [[Telepad]]
- |image = Telescience.gif
- }}
-Now, to find the bearing offset. When you teleported the GPS, you might've noticed it didn't go precisely north, although the bearing was set to 0. The bearing offset is to blame. Once again, assume the GPS travelled X tiles west and Y tiles north. Then, by dividing X by Y, you get the tangent of the offset angle, and the angle itself can be calculated as '''offset = atan(X/Y)''' (it's also integer, so feel free to round). Given the GPS travelled '''west''', that will be a positive offset that will be added to your bearing, so you have to compensate by substracting it from the bearing you will be setting. Inversly, if the GPS has gone '''east''', the offset is negative and you need to add it to the bearing.
+Well, we know that PowerOffset must be a negative number. Therefore we can remove those bars and multiply the left side of the equation by -1.
-Congratulations! Now that you know both offsets, you can teleport anything with some deadly precision or steal some high-secure items in the most stealthy fashion without having anyone see the GPS tools dancing around! So, how do you put that knowledge to use? Let's assume you want to teleport something X tiles west and Y tiles north. First, you again need to find the distance as '''sqrt(X^2 + Y^2)''' (let's designate it '''D'''). Now, set the power setting so that '''((power-offset)^2)/10''' (let's designate that number as '''Dmax''') was greater than your distance. (If you can't, you need to find you more bluespace crystals). Now, once the power is set, you need to adjust the bearing. '''Divide D by Dmax'''. As Dmax is greater, you'll get a number less than 1. You need to '''calculate the inverse sine from that number and then divide it by 2'''. In one formula,
+[[File:Telescience plugged distance equation step 4.png]]
-*elevation = (asin(D/Dmax))/2.
-Now the bearing setting is obviously dependant not only on the distances the object has to travel along the X and Y axes, but on the general direction it travels to or from (northeast, southeast, southwest, northwest). To set the bearing, you'll need to calculate '''atan(X/Y)''' if the destination is northeast or southwest, and '''atan(Y/X)''' otherwise. Both X and Y numbers here have to be positive (just the distances on X and Y axes without signs). (Writer's note: wish I could add a picture of trigonometric circle in here, that would explain everything much better than I can in words). You'll get a number between 0 and 90, which will be your bearing plus(or minus) offset if you're sending northeast. To send something along the same distances on X and Y, but in the other direction, you'll need to add a multiple of 90 degrees to it. So:
-*To send north and east, don't add anything.
-*To send south and east, add 90.
-*To send south and west, add 180.
-*To send north and west, add 270.
-Now compensate for the bearing offset, punch those numbers in the computer and hit that Send (or Recieve) button! If you're not miscalculated and everything was done right, you should now have DAT FUKKEN DISK on the telepad or a maximum-yield bomb at the AI core. Enjoy your near-omnipotence, you've truly deserved it.
-{{Item
- |bgcolor1 = #ccccee
- |bgcolor2 = #ddddff
- |name = [[Bluespace Crystal]]
- |image = Bluespace_Crystal.png
- }}
-Sadly, every 30 to 40 teleportations (roughly) the [[Telepad]] will '''fizzle'''. This means you need to click  Recalibrate and start from step 1. Learn to recalibrate quickly, or you may end up in a heap of trouble.
+Add 20 to both sides
-Leave handy beacons around the station, and GPS units at interesting locations in space, and you can easily find them again. It's worth putting something down in the [[Medbay]] so you can quickly send the wounded and the dead there.
+[[File:Telescience plugged distance equation step 5.png]]
-Also, note that the maximum radius you can reach is proportional to power squared, so, with so much as three or four extra crystals, your reach extends immensely. Just insert them into the console and higher power will become available. This also amplifies the recharge time between teleports and the energy the telepad consumes from the room's APC.
+Which is equal to -0.0031242678450383. Therefore, the power offset is 0.
 ===Challenges for the Robust in All of Us===

User:Materaspieaux: Difference between revisions